Assignment 1: Sequences and Functions#

This assignment reviews our work from the first week. As a reminder, here are the main ideas from the week:

  • Describe patterns in sequences

  • Use recursive definitions to define sequences

  • Use closed form functions to define sequences

  • Differentiate types of sequences based on how they change

Submission#

For this assignment you are to create a new google sheet in your drive. Each question should be a seperate tab in the sheet. Name the file based on your firstname_lastname_calc_assignment_I, set share settings to “anyone with link”. Questions that ask for written explanations should be included as text cells that are easily readable and formatted correctly. For help here, see here.

Problem 1: Recurrence Relations#

For each of the recurrence relations given below, generate the first 20 terms of the sequence and plot all the sequences together on the same plot.

  1. \(a_{n+1} = 2a_n + 5\) with \(a_0 = 1\)

  2. \(a_{n+1} = -a_n + 11\) with \(a_0 = 31\)

  3. \(a_{n+1} = a_n + 5n + 1\) with \(a_0 = -3\)

Problem 2: Closed Form#

For each of the functions below, use \(x = 1, 2, 3, ..., 19, 20\) to plot together on the same axes.

  1. \(f(x) = 3x+ 1\)

  2. \(f(x) = x^2 + 2x + 1\)

  3. \(f(x) = 50(1.03)^x\)

Problem 3: Fibonnacci Numbers#

Fibonnacci numbers are formed by summing the previous two values in the sequence. In general we have:

\[f_{n+1} = f_n + f_{n-1}\]

where \(f_1 = 1\) and \(f_2 = 1\). This produces the sequence:

\[1, 1, 2, 3, 5, 8, 13, ...\]

Use your spreadsheet and a new tab to generate the first 50 fibonnacci numbers. Add a column that represents the ratio of successive fibonnacci numbers and plot this column. Is anything interesting happening here?

Problem 4: Sequences from Patterns#

For each of the examples below, determine what the closed form of the pattern is, and use it to generate the first 20 terms for each of the examples on a new tab in your spreadsheet.

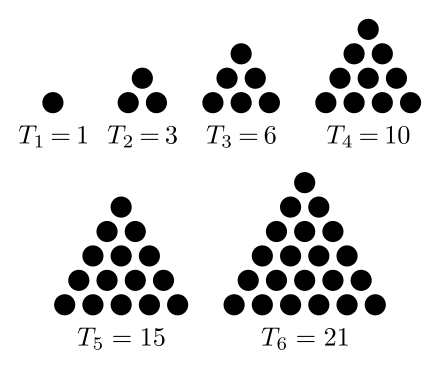
Problem 5: Triangular Numbers#

An important sequence of numbers is the Triangular numbers. Use the image below to determine a recursive definition for the sequence.

Problem 6: Online Encyclopedia of Integer Sequences#

A very nice website is the Online Encyclopedia of Integer Sequences. Please head over to the site and explore a bit. Locate a sequence of interest to you and discuss what you find including a definition of the sequence either recursive or closed form.

Problem 7: Recaman Sequence Video#

A famous example of an integer sequence that has received more modern treatment is the Recaman sequence. Please watch the video from Numberphile below and write a brief description of how the sequence looks and sounds. Can you find any other interesting sounding sequences in the encyclopedia?

from IPython.display import YouTubeVideo

YouTubeVideo(id = 'FGC5TdIiT9U', width = 600, height = 300)

Problem 8: Making a Sequence#

In the video on the Recamán sequence, the presenter said that Recamán “created” this sequence. While many sequences exist, let us pretend we don’t know and attempt to create a new sequence based on a recursive rule of your choice. After you create the sequence, search the encyclopedia for terms and names of the sequence. How does it sound? What is its name and is there any interesting history about the sequence?