More plotting with matplotlib and seaborn

Today we continue to work with matplotlib, focusing on customization and using subplots. Also, the seaborn library will be introduced as a second visualization library with additional functionality for plotting data.

#!pip install -U seaborn

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Subplots and Axes

### create a 1 row 2 column plot

### add a plot to each axis
fig, ax = plt.subplots(1, 2)

### create a 2 x 2 grid of plots
### add histogram to bottom right plot
fig, ax = plt.subplots(2, 2, figsize = (10, 8))

Exploratory Data Analysis

Exploratory data analysis (EDA) is used by data scientists to analyze and investigate data sets and summarize their main characteristics, often employing data visualization methods. – IBM

Introduction to seaborn

The seaborn library is built on top of matplotlib and offers high level visualization tools for plotting data. Typically a call to the seaborn library looks like:

sns.plottype(data = DataFrame, x = x, y = y, additional arguments...)

### load a sample dataset on tips
tips = sns.load_dataset('tips')
tips.head(2)

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3

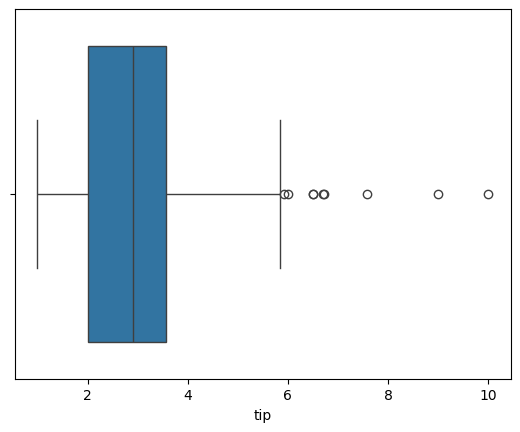
### boxplot of tips
sns.boxplot(data = tips, x = 'tip')

<Axes: xlabel='tip'>

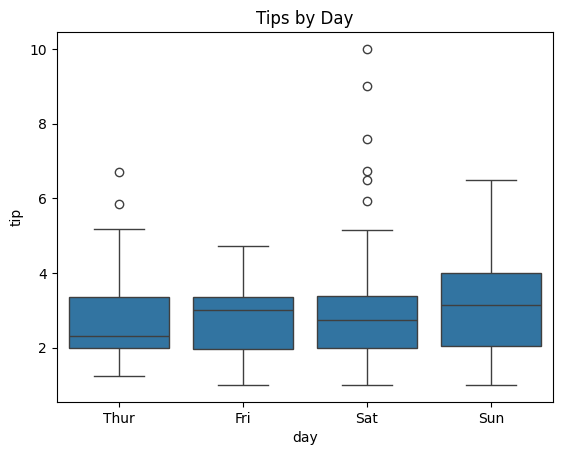
### boxplot of tips by day
sns.boxplot(data = tips, x = 'day', y = 'tip')
plt.title('Tips by Day');

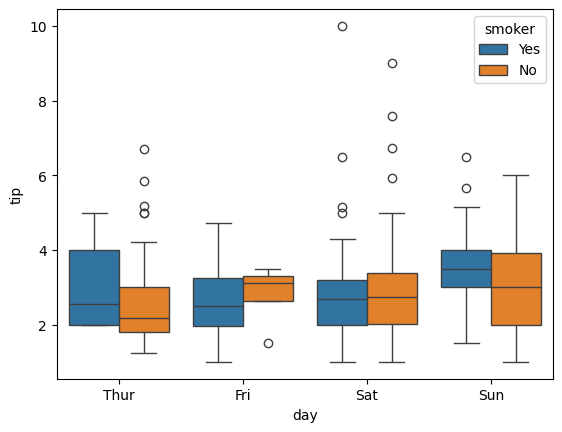
hue

The hue argument works like a grouping helper with seaborn. Plots that have this argument will break the data into groups from the passed column and add an appropriate legend.

### boxplot of tips by day by smoker
sns.boxplot(data = tips, x = 'day', y = 'tip', hue = 'smoker')

<Axes: xlabel='day', ylabel='tip'>

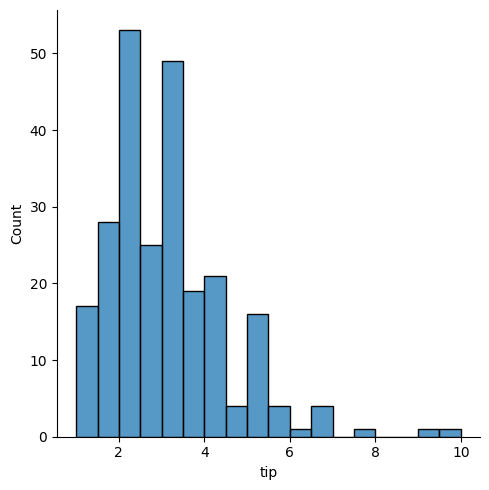
displot

For visualizing one dimensional distributions of data.

### histogram of tips
sns.displot(data = tips, x = 'tip')

<seaborn.axisgrid.FacetGrid at 0x13c888080>

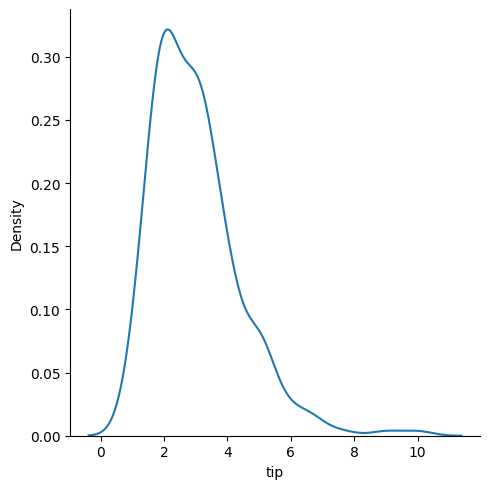
### kde plot
sns.displot(data = tips, x = 'tip', kind = 'kde')

<seaborn.axisgrid.FacetGrid at 0x13c829220>

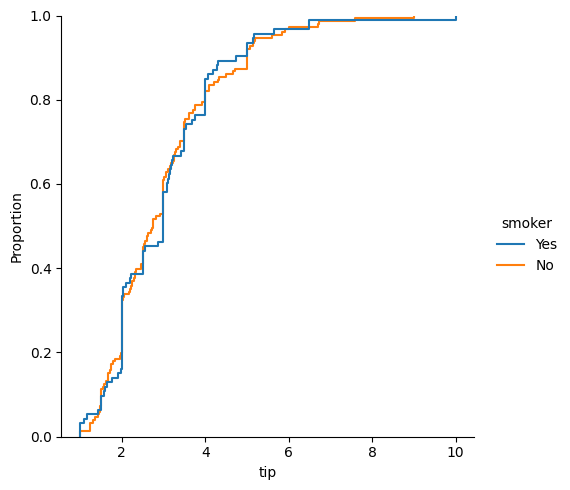
### empirical cumulative distribution plot of tips by smoker
sns.displot(data = tips, x = 'tip', kind = 'ecdf', hue = 'smoker')

<seaborn.axisgrid.FacetGrid at 0x13c6e2cf0>

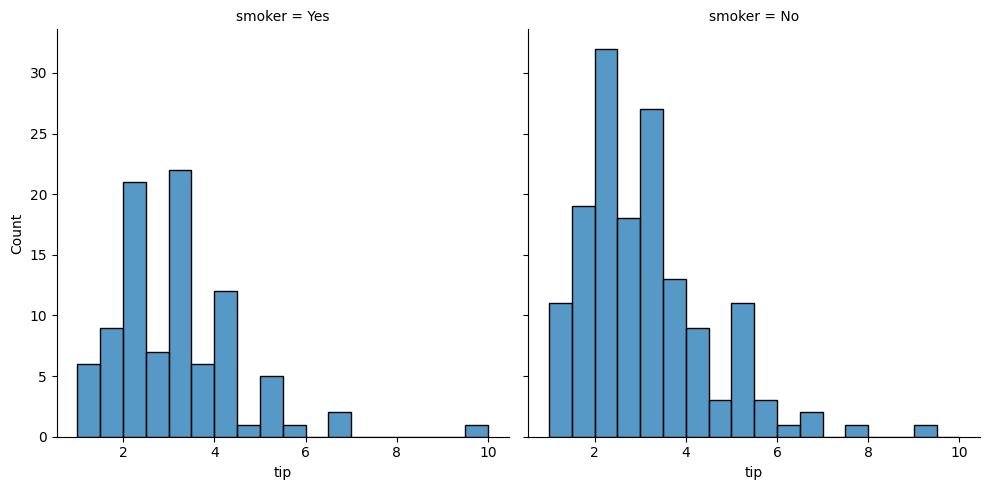
### using the col argument
sns.displot(data = tips, x = 'tip', col = 'smoker')

<seaborn.axisgrid.FacetGrid at 0x13c96c500>

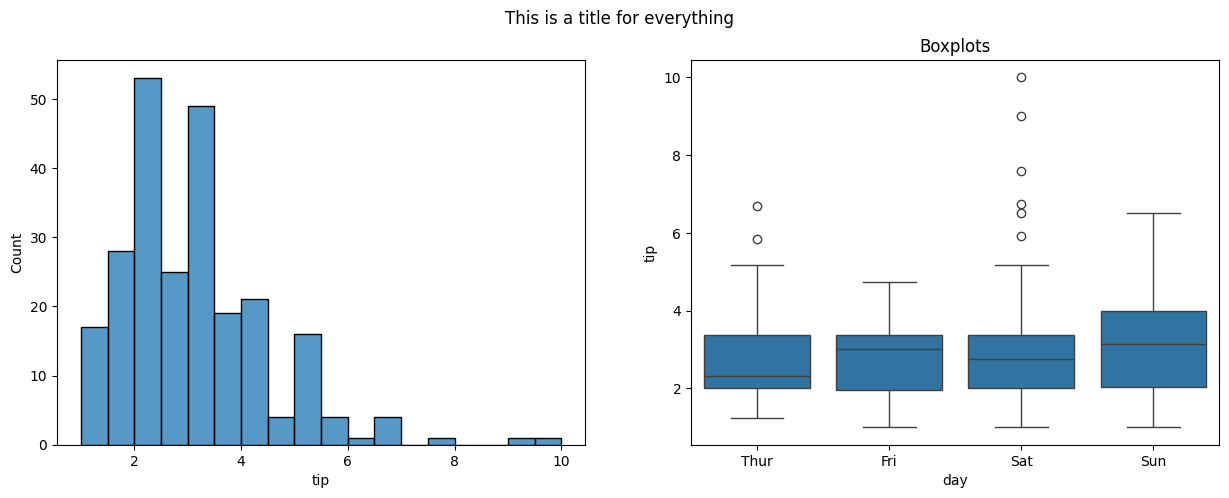
#draw a histogram and a boxplot using seaborn on two axes
fig, ax = plt.subplots(1, 2, figsize = (15, 5))
sns.histplot(data = tips, x = 'tip', ax = ax[0])
sns.boxplot(data = tips, x = 'day', y = 'tip', ax = ax[1])
ax[1].set_title('Boxplots')
fig.suptitle('This is a title for everything');

relplot

For visualizing relationships.

### relplot of bill vs. tip
sns.relplot(data = tips, x = 'total_bill', y = 'tip')

<seaborn.axisgrid.FacetGrid at 0x13ec84a40>

### regression plot
sns.regplot(data = tips, x ='total_bill', y = 'tip', lowess = True )

<Axes: xlabel='total_bill', ylabel='tip'>

### swarm
sns.swarmplot(data = tips, x = 'smoker', y = 'tip')

<Axes: xlabel='smoker', ylabel='tip'>

### violin plot
sns.violinplot(data = tips, x = 'smoker', y = 'tip')

<Axes: xlabel='smoker', ylabel='tip'>

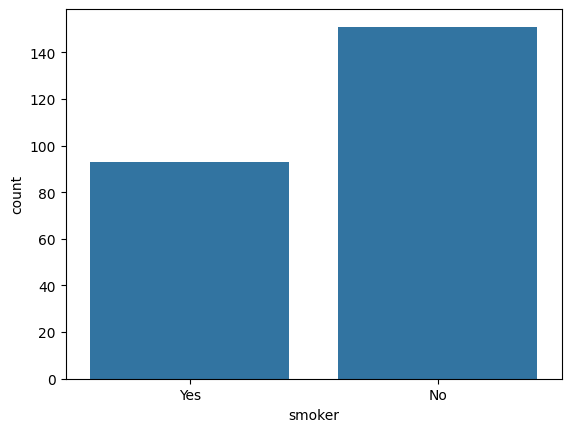
### countplot
sns.countplot(data = tips, x = 'smoker');

Additional Plots

• pairplot

• heatmap

penguins = sns.load_dataset('penguins').dropna()

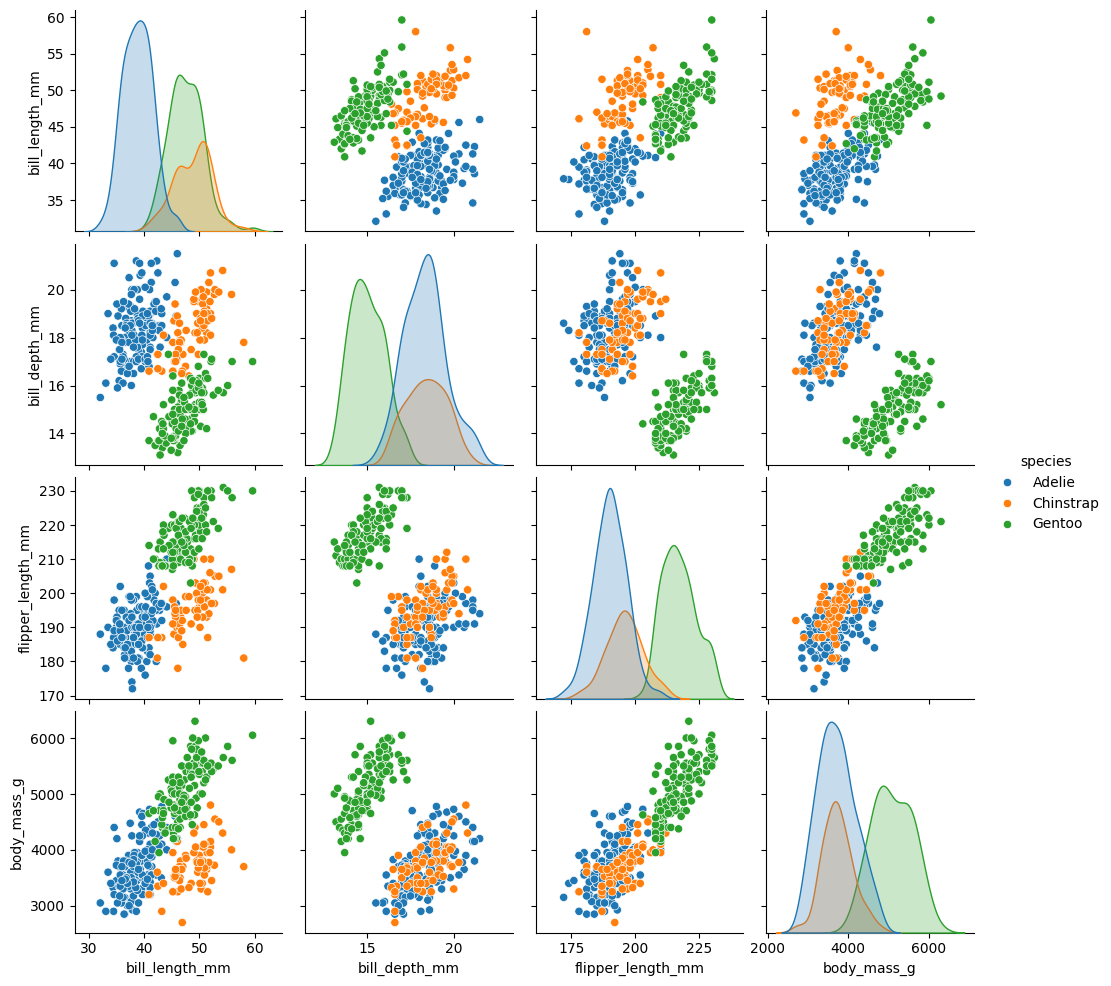
### pairplot of penguins colored by species
sns.pairplot(data = penguins, hue = 'species', diag_kind = 'kde')

<seaborn.axisgrid.PairGrid at 0x1473f30b0>

### housing data
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing(as_frame = True).frame
housing.head()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude	MedHouseVal
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23	4.526
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22	3.585
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24	3.521
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25	3.413
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25	3.422

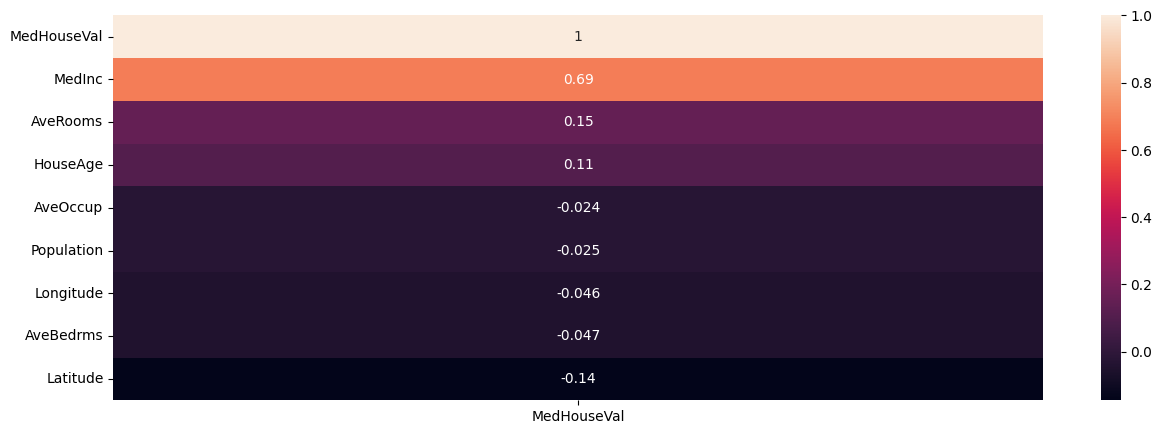
Plotting Correlations

Correlation captures the strength of a linear relationship between features. Often, this is easier to look at than a scatterplot of the data to establish relationships, however recall that this is only a detector for linear relationships!

### correlation in data
housing.corr(numeric_only = True)

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude	MedHouseVal
MedInc	1.000000	-0.119034	0.326895	-0.062040	0.004834	0.018766	-0.079809	-0.015176	0.688075
HouseAge	-0.119034	1.000000	-0.153277	-0.077747	-0.296244	0.013191	0.011173	-0.108197	0.105623
AveRooms	0.326895	-0.153277	1.000000	0.847621	-0.072213	-0.004852	0.106389	-0.027540	0.151948
AveBedrms	-0.062040	-0.077747	0.847621	1.000000	-0.066197	-0.006181	0.069721	0.013344	-0.046701
Population	0.004834	-0.296244	-0.072213	-0.066197	1.000000	0.069863	-0.108785	0.099773	-0.024650
AveOccup	0.018766	0.013191	-0.004852	-0.006181	0.069863	1.000000	0.002366	0.002476	-0.023737
Latitude	-0.079809	0.011173	0.106389	0.069721	-0.108785	0.002366	1.000000	-0.924664	-0.144160
Longitude	-0.015176	-0.108197	-0.027540	0.013344	0.099773	0.002476	-0.924664	1.000000	-0.045967
MedHouseVal	0.688075	0.105623	0.151948	-0.046701	-0.024650	-0.023737	-0.144160	-0.045967	1.000000

### heatmap of correlations
plt.figure(figsize = (15, 5))
sns.heatmap(housing.corr(numeric_only=True)[['MedHouseVal']].sort_values(by = 'MedHouseVal', ascending = False), annot = True)

<Axes: >

Problems

Use the diabetes data below loaded from OpenML (docs).

from sklearn.datasets import fetch_openml

diabetes = fetch_openml(data_id = 37).frame

diabetes.head()

	preg	plas	pres	skin	insu	mass	pedi	age	class
0	6	148	72	35	0	33.6	0.627	50	tested_positive
1	1	85	66	29	0	26.6	0.351	31	tested_negative
2	8	183	64	0	0	23.3	0.672	32	tested_positive
3	1	89	66	23	94	28.1	0.167	21	tested_negative
4	0	137	40	35	168	43.1	2.288	33	tested_positive

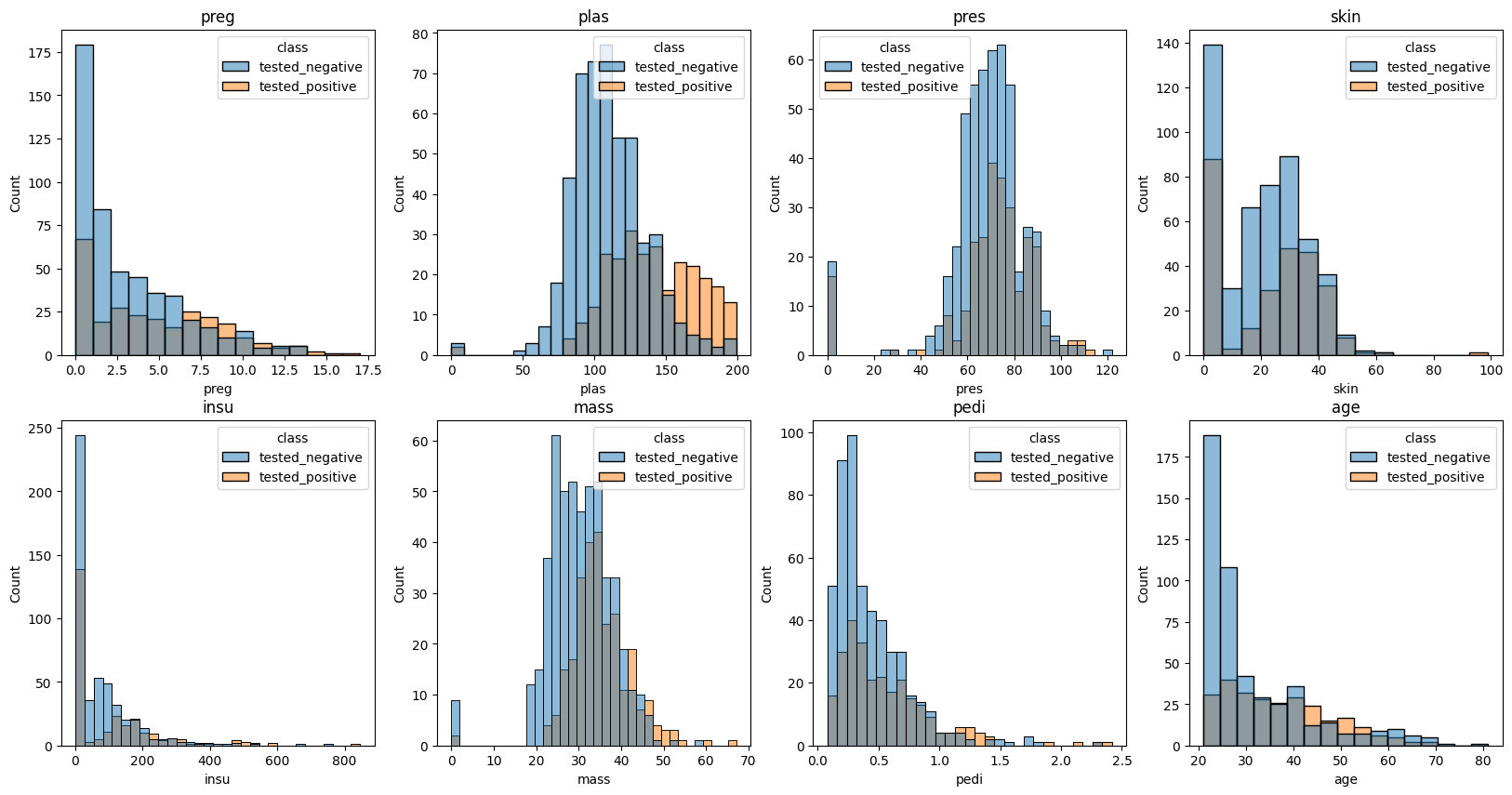
1. Plot distribution of ages separated by class.

2. Use the plots below to determine which feature has the most distinct difference between classes?

fig, ax = plt.subplots(2, 4, figsize = (20, 10))
colnum = 0
for row in range(2):
    for col in range(4):
        sns.histplot(data = diabetes, x = diabetes.iloc[:,colnum], hue = 'class', ax =  ax[row, col])
        ax[row,col].set_title(diabetes.columns.tolist()[colnum])
        colnum += 1

3. Head over the the seaborn documentation here. Find a different plot type or function and implement it using the diabetes data.

Partner Exercise

• What time of year is most popular for bike rentals?

• What’s the most popular day of the week for bike rentals?

• What’s the frequency of use for the average user?

• What are the most and least congested bike stations?

bikeshare_hour = pd.read_csv('data/hour.csv')

bikeshare_hour.head()

	instant	dteday	season	yr	mnth	hr	holiday	weekday	workingday	weathersit	temp	atemp	hum	windspeed	casual	registered	cnt
0	1	2011-01-01	1	0	1	0	0	6	0	1	0.24	0.2879	0.81	0.0	3	13	16
1	2	2011-01-01	1	0	1	1	0	6	0	1	0.22	0.2727	0.80	0.0	8	32	40
2	3	2011-01-01	1	0	1	2	0	6	0	1	0.22	0.2727	0.80	0.0	5	27	32
3	4	2011-01-01	1	0	1	3	0	6	0	1	0.24	0.2879	0.75	0.0	3	10	13
4	5	2011-01-01	1	0	1	4	0	6	0	1	0.24	0.2879	0.75	0.0	0	1	1