The Problem of Areas#

import matplotlib.pyplot as plt
import numpy as np

Problem 1: Parabola#

Consider the area under the curve:

$$f(x) = -x^2 + 4$$ from $x = -1$ until $x = 1$

#define the function

#domain from -2.5 to 2.5

#plot the function with grid and color the region

Using Rectangles#

The first approach we will use is to build a small number of rectangles to approximate the area.

What are the $x$ coordinates for these rectangles if we use 4 rectangles with equal spacing?
What would the height of the rectangles be and why?
Find the area of each rectangle.
Add these areas together.

#x values

#heights?

#areas

#total area approx

Improving the Approximation#

Use 8 rectangles and repeat the example above.

What are the $x$-coordinates for each rectangle
What is the height of the rectangle
What is the area of each rectangle
What is the total area of each rectangle.

#x-values

#width of each rectangle?

#heights

#areas

#total areas

Problem#

Use 16 rectangles and repeat above.

#x coordinates

#heights

#areas

#total area

QUESTIONS

Which of these was the best approximation and why?
Repeat the above process to estimate the area under the given curves with given boundaries:

$f(x) = \sin{x}$ on $[0, 2\pi]$. Draw a plot of the region, and start with 4 rectangles to approximate the area under the curve.

Human Work#

House-painting is a job that can be done by several people working simultaneously, so we can measure the amount of work done in staff-hours. Consider a house-painting business run by some students. Because of class schedules, different numbers of students will be painting at different times of the day. Let $s(t)$ be the number of staff present at time $t$, measured in hours from 8 am, and suppose that during an 8-hour work day, we have:

\[\begin{split}s(t) = \begin{cases} 3 & 0 \leq t < 2 \\ 2 & 2 \leq t < 4.5 \\ 4 & 4.5 \leq t \leq 8 \end{cases}\end{split}\]

def s(t):
    return np.piecewise(t,
                 [t < 2, t > 2, t > 4.5], 
                 [3, 2, 4])

t = np.linspace(0, 8, 1000)

s(t)[::100]

array([3., 3., 3., 2., 2., 2., 4., 4., 4., 4.])

plt.plot(t, s(t))
plt.grid()
plt.title('Work Hours at Time $t$')
plt.ylim(0, 5);

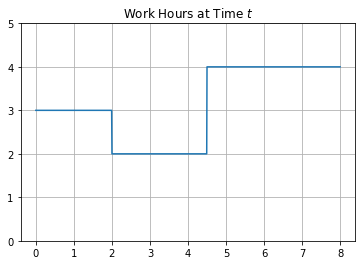
What is the total number of staff hours worked at times $t = 1, 2, 3, 4, 5, 6, 7, 8$?

Suppose that there is a house-painting job to be done, and by past experience the students know that four of them could finish it in 6 hours. But for the first 3.5 hours, only two students can show up, and after that, five will be available.

a. How long will the entire job take? b. Draw a graph of he staffing function for this problem. Mark on the graph when the job is finished. c. Draw the graph of the accumulated work function.

Problem: Computing Distance Traveled#

Suppose you are traveling in a vehicle that moves at the following speed in miles per hour at given time $t$ (in hours):

\[\begin{split}v(t) \begin{cases} 10 & t < 3 \\ 2t & 3 \leq t \leq 5 \\ 20 & t > 5 \end{cases}\end{split}\]

How far would you travel in the first hour?
2 hours?
3 hours?
5 hours?
10 hours?

How much energy consumed#

Use the table below where the power demand for a house is given at time $t$.

$t$	power
1:30	275
5:00	240
8:00	730
9:30	300
11:00	150
15:00	225
18:30	1880
20:00	950
22:30	700
23:00	350

Calculus I

The Problem of Areas

Contents