Regression Part II

OBJECTIVES

• Use sklearn to build multiple regression models

• Use statsmodels to build multiple regression models

• Evaluate models using mean_squared_error

• Interpret categorical coefficients

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

Using Many Features

The big idea with a regression model is its ability to learn parameters of linear equations.

\[y = \beta_0 + \beta_1x \quad and \quad y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \dots\]

\[\begin{split}\begin{bmatrix} 1 & 3.2 & 4 \\ 1 & 5.2 & 3 \\ 1 & 4.1 & 3.4 \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix} = \begin{bmatrix} 12 \\ 10.4 \\ 9.7 \end{bmatrix}\end{split}\]

\[X\beta =y\]

\[\beta = (X^TX)^{-1}X^Ty\]

tips = sns.load_dataset('tips')

X = tips['total_bill'].values.reshape(-1, 1)
y = tips['tip'].values.reshape(-1, 1)

#column of ones for intercept
intercept = np.ones(shape = X.shape)
#design matrix contains leading column of ones
design_matrix = np.concatenate((intercept, X), axis = 1)

design_matrix[:5]

array([[ 1.  , 16.99],
       [ 1.  , 10.34],
       [ 1.  , 21.01],
       [ 1.  , 23.68],
       [ 1.  , 24.59]])

#linear algebra solution to least squares
np.linalg.inv(design_matrix.T@design_matrix)@design_matrix.T@y

array([[0.92026961],
       [0.10502452]])

Advertising Data

The goal here is to predict sales. We have spending on three different media types to help make such predictions. Here, we want to be selective about what features are used as inputs to the model.

ads = pd.read_csv('https://raw.githubusercontent.com/jfkoehler/nyu_bootcamp_fa25/main/data/ads.csv', index_col=0)

ads.head()

	TV	radio	newspaper	sales
1	230.1	37.8	69.2	22.1
2	44.5	39.3	45.1	10.4
3	17.2	45.9	69.3	9.3
4	151.5	41.3	58.5	18.5
5	180.8	10.8	58.4	12.9

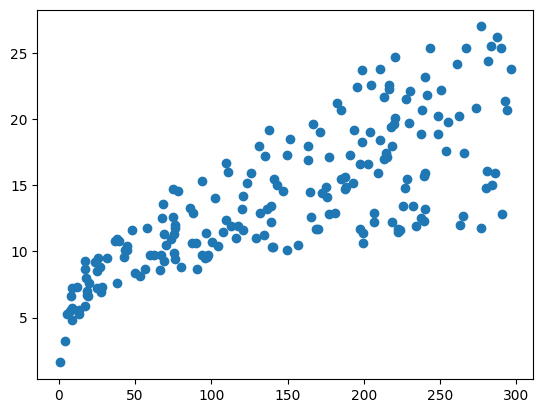
#scatterplot
plt.scatter(ads['TV'], ads['sales']);

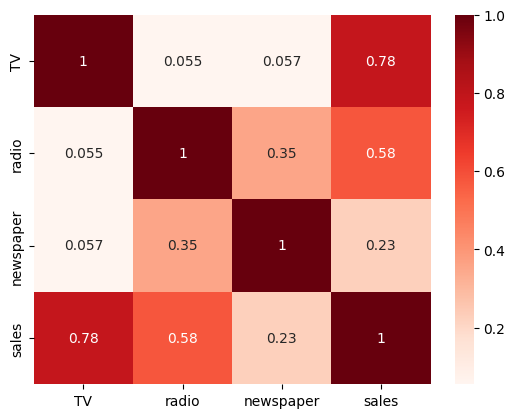
# heatmap
sns.heatmap(ads.corr(), annot = True, cmap = 'Reds');

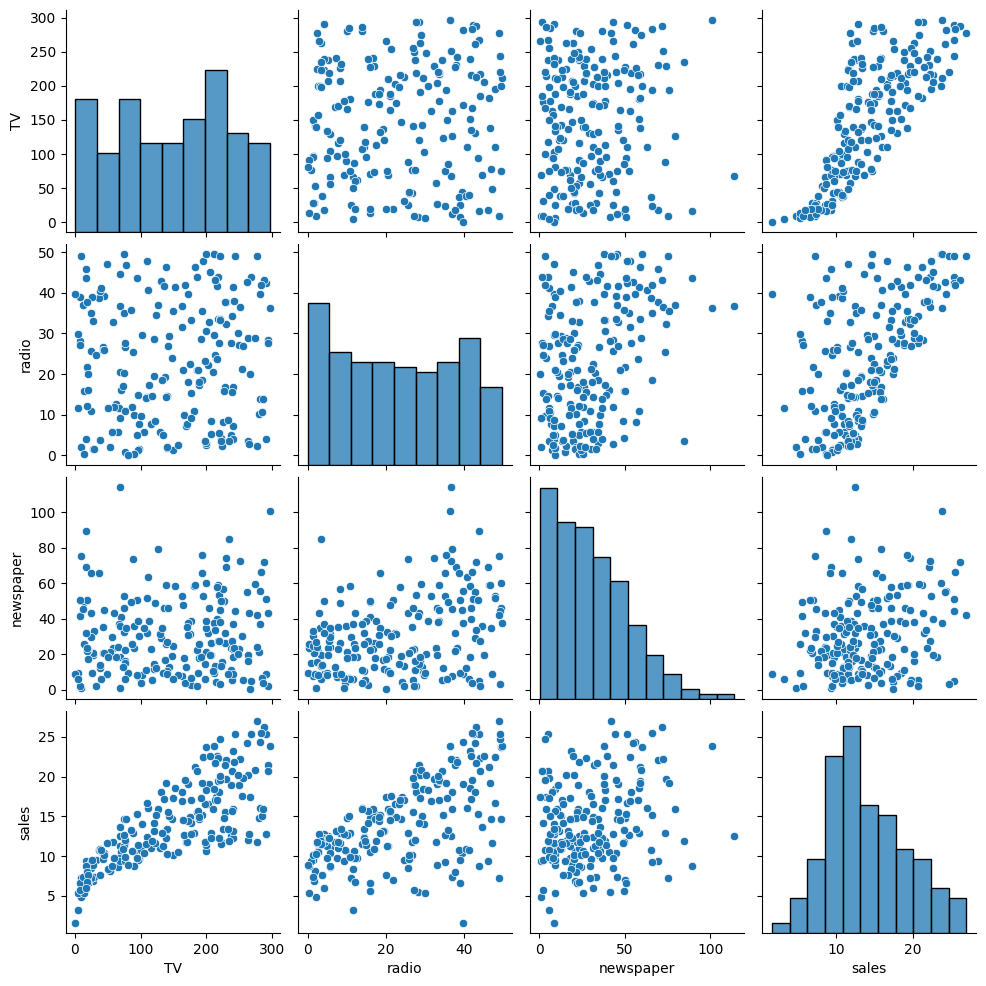
# pairplot
sns.pairplot(ads);

1. Choose a single column as X to predict sales. Justify your choice – remember to make X 2D.

#declare X and y
X = ''
y = ''

2. Build a regression model to predict sales using your X above.

# instantiate and fit the model
model1 = ''

3. Interpret the slope of the model.

# examine slope, what does it mean?

4. Interpret the intercept of the model.

#intercept

5. Determine the mean_squared_error of the model.

from sklearn.metrics import mean_squared_error

# MSE

6. Create baseline predictions using the mean of y. (Try the DummyRegressor here).

from sklearn.dummy import DummyRegressor

7. Compute the mean_squared_error of your baseline predictions.

# MSE Baseline

8. Did your model perform better than the baseline?

9. What does the PredictionErrorDisplay object do? Can you demonstrate its use?

from sklearn.metrics import PredictionErrorDisplay

the .score method

In addition to the mean_squared_error function, you are able to evaluate regression models using the objects .score method. This method evaluates in terms of \(r^2\). One way to understand this metric is as the ratio between the residual sum of squares and the total sum of squares. These are given by:

\[RSS = \sum _{i}(y_{i}-f_{i})^{2}\]

\[TSS = \sum _{i}(y_{i}-{\bar {y}})^{2}\]

and

\[r^2 = 1 - \frac{RSS}{TSS}\]

#model score

You can interpret this as the percent of variation in the data explained by the features according to your model.

Adding Features

Now, we want to include a second feature as input to the model. Reexamine the plots and correlations above, what is a good second choice?

9. Choose two columns from the ads data, assign these as X.

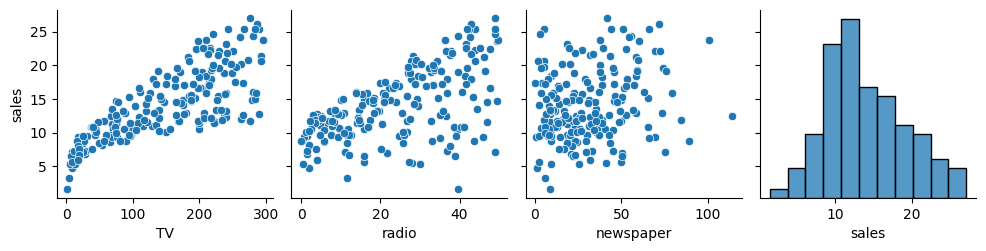
sns.pairplot(ads, y_vars = 'sales')

<seaborn.axisgrid.PairGrid at 0x13b68f980>

# X2
X2 = ads[['']]

10. Build a regression model with two features to predict sales.

# lr2 model

11. Evaluate the model using mean_squared_error.

# yhat2

# MSE

12. Interpret the coefficients of the model

# make a dataframe here

Example II: California Housing Data

cali = pd.read_csv('https://raw.githubusercontent.com/ageron/data/refs/heads/main/housing/housing.csv')
cali.head()

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY

# !pip install folium

import folium

from folium.plugins import HeatMap

m = folium.Map(cali[['latitude', 'longitude']].values[0])
HeatMap(cali[['latitude', 'longitude', 'median_house_value']].values, blur = 1, radius = 5).add_to(m);

m

Make this Notebook Trusted to load map: File -> Trust Notebook

#what features do you think matter?

#any new features we can manufacture?

#any features to encode?

#any missing data?